语言模型与词向量基础

1. 语言模型基础与词向量

语言模型可以简单理解为一个句子 s 在所有句子中出现的概率分布 P(s)。比如一个语料库中有100 个句子，『OK』这个句子出现了5次， 那么 $p(OK) = 5\%$。

那么，如何学习到这种概率分布呢？ 最简单的方法是建立一个无比庞大的语料库，该语料库中包含了人类成百上千年间可能讲过的所有的话，那么我们不就可以算出这句话出现的概率了吗。可惜此方法不现实。

那么，能不能通过数学的方法进行表示呢？答案是可以滴，因为 S 是一个序列 $w_1, w_2 , \cdots ,w_n$，那么$p(s)$可以展开为：

$$p(s) = P(w_1, w_2, \cdots, w_n) = P(w_1) \cdot P(w_2|w_1) \cdot P(w_3|w_1,w_2) \cdots P(w_n|w_1, w_2, \cdots, w_{n-1})$$

那么现在的问题就变成了我们如何计算 $P(w_1, w_2, \cdots, w_n) $

2. 统计方法 - n元模型

我们观察上式，会发现， $P(w1)$ 比较好算， $P(w_2|w_1)$ 也还ok， $P(w_3|w_1,w_2)$ 就比较有难度了，随着n的增大，计算会越来越难， $P(w_n|w_1, w_2, \cdots, w{n-1})$ 几乎根本不可能估算出来。怎么办？

马尔可夫假设：假设任意一个词 $wi$ 出现的概率只同它前面的n个词 $(w{i-1}, \cdots, w_{i-n})$ 有关。由此，那么就有：

$$一元模型： P(S) = \prod_{i=1}^{l} P(w_i) \\ 二元模型：P(S) = \prod_{i=1}^{l} P(w_i|w_{i-1})$$

缺陷：

1. 无法建模更远的关系，语料的不足使得无法训练更高阶的语言模型。
2. 无法建模出词之间的相似度。
3. 训练语料里面有些 n 元组没有出现过,其对应的条件概率就是 0,导致计算一整句话的概率为 0。解决这个问题有两种常用方法： 平滑法和回退法。

3. 深度学习方法 - 神经网络语言模型[1]

首先，我们回到问题本身，我们为什么要计算 $p(s)$， 我们的目的是为了通过大规模语料库学习到语言内部的概率分布。那么有没有办法通过深度学习的方式来学习到这种概率分布呢？

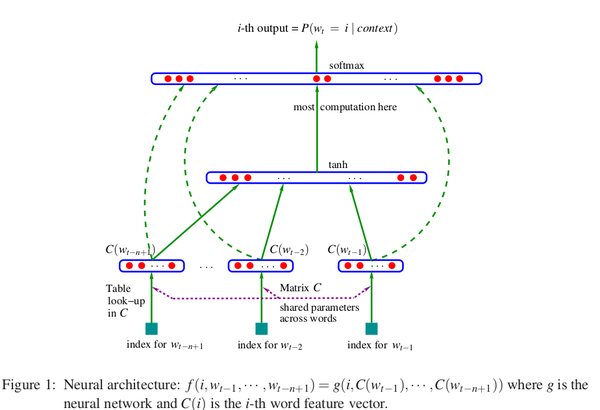
观察上图，假设有一组词序列： $w_1, w_2, \cdots, w_t$ ，其中 $w_i \in V$ ， $V$ 是所有单词的集合。我们的输入是一个词序列，而我们的输出是一个概率值，表示根据context预测出下一个词是 $i$ 的概率。用数学来表示，我们最终是要训练一个模型：

$$P(w_t = i | context) = P(w_t | w_1^{t-1})$$

• $wt $表示这个词序列中的第 $t$ 个单词， $w{t-n+1}$ 表示输入长度为n的词序列中的第一个单词
• $w_1^{t-1}$ 表示从第1个单词到第 $t-1$ 个单词组成的子序列

因此我们发现，该模型的每个样本其实计算的是：$