词向量

---

https://zhuanlan.zhihu.com/p/29364112

Word2Vec[3]

Word2Vec是Google发布的一个工具， 用于训练词向量，其提供了两种语言模型来供选择， 且Google 基于大规模语料集上训练出了预训练词向量来供开发者或研究者使用。 一般情况下，我们是没有必要自己去训练词向量的，但如果要求特殊，且语料集庞大，自己训练也是可以的。

在Word2Vec中，实现了两个模型：CBOW 与 Skip-Gram。

1. CBOW模型

CBOW，全称Continuous Bag-of-Word，中文叫做连续词袋模型：以上下文来预测当前词 $w_t$ 。

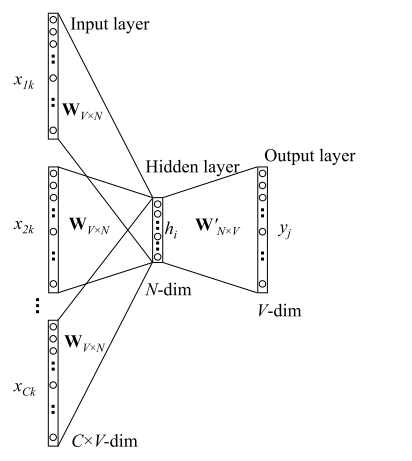
如上图是一个两层的神经网络，其实在训练语言模型的过程中考虑到效率等问题，常常采用浅层的神经网络来训练，并取第一层的参数如上图就是 $W_{V \times N}$ 来作为最终的词向量矩阵（参考 语言模型：从n元模型到NNLM）。

CBOW模型的目的是预测 $P(wt| w{t-k}, \cdots, w{t-1}, w{t+1}, \cdots, w_{t+k}) $，我们先来走一遍CBOW的前向传播过程 。

1. 前向传播过程

• 输入层: 输入C个单词： $x{1k}, \cdots, x{Ck} $，并且每个 $x$ 都是用 One-hot 编码表示，每一个 $x$ 的维度为 V（词表长度）。

• 输入层到隐层: 共享矩阵为 $W_{V \times N}$ ，V表示词表长度，W的每一行表示的就是一个N维的向量（训练结束后，W的每一行就表示一个词的词向量）。在隐藏层中，我们的所有输入的词转化为对应词向量，然后取平均值，这样我们就得到了隐层输出值 ( 注意，隐层中无激活函数，也就是说这里是线性组合)。 其中，隐层输出 $h$ 是一个N维的向量 。

  $$h = \frac{1}{C} W^T(x_1 + x_2 + \cdots + x_c)$$

• 隐层到输出层：隐层的输出为N维向量 $h$ ， 隐层到输出层的权重矩阵为 $W’_{N \times V}$ 。然后，通过矩阵运算我们得到一个 $V \times 1 $ 维向量

  $$u = W'^{T} * h$$

其中，向量 $u$ 的第 $i$ 行表示词汇表中第 $i$ 个词的可能性，然后我们的目的就是取可能性最高的那个词。因此，在最后的输出层是一个softmax 层获取分数最高的词，那么就有我们的最终输出：

$$P(w_j| context) =y_i = \frac{exp({u_j})}{\sum_{k \in V} exp({u_k})}$$

2. 损失函数

我们假定 $j^*$ 是真实单词在词汇表中的下标，那么根据极大似然法，则目标函数定义如下：

$$E = -log \, p(W_O |W_I) = -log \, \frac{exp({u_j})}{\sum_{k \in V} exp({u_k})} = log \, \sum_{k \in V} exp(u_{k}) -u_j$$

2. Skip-gram模型

Skip-Gram的基本思想是：已知当前词 $wt$ 的前提下，预测其上下文 $w{t-i}, \cdots , w_{t+i}$ ，模型如下图所示：

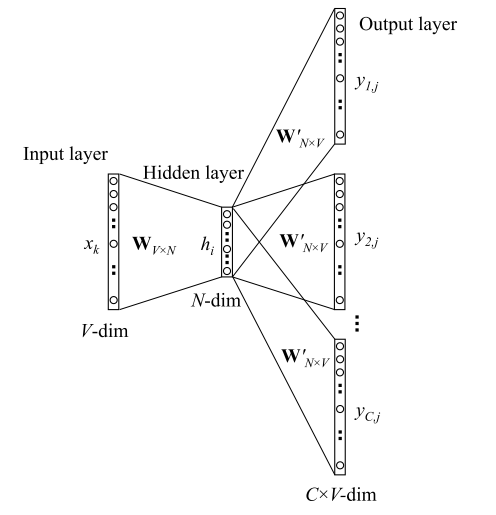
1. 前向传播过程：

• 输入层： 输入的是一个单词，其表示形式为 One-hot ，我们将其表示为V维向量 $xk$ ，其中 $V$ 为词表大小。然后，通过词向量矩阵 $W{V \times N}$ 我们得到一个N维向量 $$h = W^T * x_k = v^{T}_{w_I}$$

• 隐层： 而隐层中没有激活函数，也就是说输入=输出，因此隐藏的输出也是 $h$ 。

• 隐层到输出层：

  • 首先，因为要输出C个单词，因此我们此时的输出有C个分布： $y_1, \cdots y_C $，且每个分布都是独立的，我们需要单独计算， 其中 $y_i$ 表示窗口的第 $i$ 个单词的分布。
  • 其次， 因为矩阵 $W’{N \times V}$ 是共享的，因此我们得到的 $V \times 1$ 维向量 $u$ 其实是相同的，也就是有 $u{c,j} = u_j$ ，这里 $u$ 的每一行同 CBOW 中一样，表示的也是评分。
  • 最后，每个分布都经过一个 softmax 层，不同于 CBOW，我们此处产生的是第 $i$ 个单词的分布（共有C个单词），如下：

  $$P(w_{i,j}| context) =y_i = \frac{exp({u_j})}{\sum_{k \in V} exp({u_k})}$$

2. 损失函数

假设 $j^*$ 是真实单词在词汇表中的下标，那么根据极大似然法，则目标函数定义如下：

$$\begin{split} E &= - log \, p(w_1, w_2, \cdots, w_C | w_I) \\ &= - log \prod_{c=1}^C P(w_c|w_i) \\ &= - log \prod_{c=1}^{C} \frac{exp(u_{c, j})}{\sum_{k=1}^{V} exp(u_{c,k}) } \\ &= - \sum_{c=1}^C u_{j^*_c} + C \cdot log \sum_{k=1}^{V} exp(u_k) \end{split}$$

3. 模型复杂度

本节中我们来分析一下模型训练时的复杂度，无论是在CBOW还是Skip-Gram模型中，都需要学习两个词向量矩阵： $W, W’$ 。

对于矩阵 $W$ ， 从前向传播中可以看到， 可以看到对于每一个样本(或mini-batch)，CBOW更新 $W$ 的 C 行（h与C个x相关）， 而Skip-Gram 更新W中的其中一行（h与1个x相关），这点训练量并不算大。

对于 $W’$ 而言， 无论是 CBOW 还是 Skip-Gram 模型，每个训练样本(mini-batch)都更新 $W’$ 的所有 $V \times N$ 个元素。

在现实中，用于语言模型训练的数据集通常都很大，此外词表也是巨大的，这就导致对于 $W’$ 的更新所花费的计算成本是很大的，真的是验证了一个道理：穷逼必要搞语言模型。

为了解决优化起来速度太慢的问题， Word2Vec 中提供了两种策略来对这方面进行优化。

4. Hierarchical Softmax

HS 基于哈夫曼树将计算量大的部分转化为一种二分类问题。

原先的模型中，模型再隐层之后通过 $W’$ 连接输出层，现在 HS 则去掉了 $W’$ , 隐层向量 h 直接与上图的二叉树的 root 节点相连， 图中的每一个分支都代表一个选择。 上图中白色的叶子节点表示词表中所有的$|V|$个词， 黑色节点表示非叶子节点， 每一个叶子节点（单词）都对应一条从 root 节点出发的路径，而问题就转化为了使得 $w=w_o$ 这条路径的概率最大， 即：$P(w=w+O|w_I)$ 最大。

用 $n(w,j)$ 表示从 root 到叶子节点 w 的路径上的第 j 个非叶子节点, 并且每个非叶子节点都对应一个向量$v_{n(w,j)}′$, 维度与h 相同, 然后使用一个sigmod函数: $σ(x)=\frac{1}{1+exp(−x)}∈[0,1]$ ，结合向量的内积, 来判断该向左还是向右，那么第 n 个节点向左以及向右的概率分别为：

$$P(n,left) = \sigma(v_w' \cdot h) \\ P(n, right) = 1 - \sigma(v_w' \cdot h)$$

那么就有：

$$P(w=w_O|W_I) = \prod_{j=1}^{L(w)-1} P(\sigma(I(n(w, j+1 == left) v_w' \cdot h))$$

• $I()$ ：指示函数，条件成立值为1， 反之为 -1
• $L(w)$ ：表示整条路径的长度

这样我们就能够通过训练来更新每个非叶子节点的参数 $v_w’$了。举例来说，图上加黑的黑色路径： $(n(w_2,1),n(w_2,2),n(w_2,3),w2$， 对于一个训练样本，我们要使得 $P(w_O=w_2|w_I)$ 概率最大：

$$P(w_2=w_O) = P(n(w_2, 1), left) \cdot P(n(w_2, 2), left) \cdot P(n(w_2, 3), right)$$

且需要注意的时，再一个非叶子节点处， 向左向右的概率和为1， 因此一直分裂下去，最后的和肯定还是1， 因此可以得出：

$$\sum_{j=1}^V P(w_j = w_O) = 1$$

损失函数同样为最大似然：

$$E = -log P(w = w_O | w_I) = -\sum_{j=1}^{L(w) -1} log \sigma([I] v_j'^Th)$$

通过 HS， 隐层到输出层的计算量从 $O(V)$ 降到了 $O(logV)$。

2. Negative Sampling — 负采样

在 Word2Vec 中， 对于输出层来说，我每一个输出节点都要预测词表中所有词在当前位置的概率，在动辄几万甚至几十万大的词表中，用softmax 计算真的十分困难。

但我们的目的不在于训练一个精准的语言模型，而只是为了训练得到语言模型的副产物-词向量，那么我们可不可以把输出压缩呢，将几万的输出压缩到几十程度，这计算量是成几何倍数的下降。

负采样的思路很简单，不直接让模型从整个词表中找最可能的词，而是直接给定这个词（正例）和几个随机采样的噪声词（负例），然后模型能够从这几个词中找到正确的词，就算达到目的了。

那么如何对负例进行采样呢？作者直接使用基于词频的权重分布来获得概率分布进行抽样：

$$weight(w) = \frac{count(w)^{0.75}}{\sum_u count(w)^{0.75}}$$

相比于直接使用频次作为权重， 取0.75幂的好处可以减弱不同频次差异过大带来的影响，使得小频次的单词被采样的概率变大。

此时的损失函数为：

$$E = - log \sigma(v_{w_O}' h) - \sum_{w_j \in W_{neg}} log \sigma(-v_{w_j}'h)$$

Glove []

Questions

Reference Papers

[1] Mikolov, T.(2013). Distributed Representations of Words and Phrases and their Compositionality.

[2] Mikolov, T.(2013). Efficient Estimation of Word Representations in Vector Space.

[3] Rong, X. (2014). word2vec Parameter Learning Explained.

[4] GloVe: Global Vectors for Word Representation

[5] Enriching Word Vectors with Subword Information

[6] Bag of Tricks for Efficient Text Classification